de los métodos, a excepción del empleo
de la piedra imán
Johann Tesnerius, arzobispo de Colonia, siglo XVI
Hipótesis
Ya sabemos que dos imanes ejercen entre sí fuerzas atractivas, fuerzas repulsivas y fuerzas de torca. Concentremos nuestra atención en las terceras. Imagine que con una mano sostiene firmemente un imán y que éste en su tendencia natural a unirse a otro imán experimenta fuerzas que tratan de girarlo sobre sí mismo. A continuación deja que el imán gire lentamente sobre sí mismo y cuando la línea que atraviesa sus polos queda en posición perpendicular con respecto a la línea vertical que atraviesa los polos del otro imán usted detiene el giro. En esta situación de inmovilidad ¿le parece que el imán puede desplazarse linealmente? Veamos, ¿las fuerzas de atracción y repulsión que están actuando sobre los polos son perfectamente paralelas entre sí? Dígamos que no. Pienso que el concepto de par de fuerzas es aplicable a las bobinas pero poco realista en el caso de los imanes permanentes al excluir esta posibilidad. Ahora bien, ¿esas dos fuerzas de torca no paralelas entre sí pueden producir un movimiento rectilíneo? Sólo deben tener componentes horizontales con la misma dirección y sentido para hacerlo. En el estado de inmovilidad descrito ¿aquellas componentes parecen ser capaces de generar un movimiento lineal? Obviamente que sí, puesto que se trata de fuerzas aplicadas continuamente en una misma dirección y sentido. Pero, ¿qué podemos hacer para evitar el giro del imán sin impedir al mismo tiempo su movimiento lineal? A primera vista la respuesta parece ser simple... encarrilar el imán.
En este blog propongo la hipótesis de que las fuerzas magnéticas de torca, además de producir el típico movimiento giratorio de un imán sobre sí mismo cuando éste está libre, tienen componentes que son capaces de mover un imán siguiendo una dirección única cuando el imán permanece dentro de un carril rectilíneo.
Al tratarse de las fuerzas magnéticas que producen la torca, el ángulo entre los imanes no se restringe únicamente a un valor de 90º sino que puede adoptar cualquiera de los valores mayores a 0º y menores a 180º. Cómo referencia, a 0º uno de los polos del imán que es girado en torno a su propio centro se encontraría paralelo al polo del otro imán y a 180º se encontraría paralelo en cambio el polo opuesto del imán girado.
La idea de encauzar las componentes de las fuerzas magnéticas que dan origen a la torca conduce a un sencillo experimento realizado con un imán grande y fijo y otro pequeño y encarrilado.
Experimento básico
Para comprobar lo dicho consigamos dos imanes de ferrita: uno rectangular de 47,6 mm x 22,2 mm x 9,5 mm y otro redondo de 12 mm de diámetro y 6 mm de grosor (fig. 1).
Procedamos a fijar el imán redondo en el centro de una tira de madera de balsa de por ejemplo 130 mm x 22,2 mm x 6 mm, para lo cual envolveremos juntos el imán redondo y la parte central de la tira de madera con cinta adhesiva (dos vueltas de la cinta serán suficientes). Los polos del imán redondo deben quedar apuntando hacia los extremos de la tira de madera. Coloquemos el imán rectangular sobre una mesa y frente a él una regla, estos dos elementos conformaran el carril. El imán rectangular se mantiene fijo con los dedos de la mano izquierda. Con los dedos de la mano derecha agarremos la tira que lleva el imán redondo por uno de sus extremos y juntemos la cara libre de la tira al polo del imán rectangular. El borde numerado de la regla debe encontrarse debajo de la mitad del imán redondo; el borde de la regla no hace contacto con la cinta adhesiva, sólo sirve para detener el imán redondo cuando este tiende a separare del imán rectangular. Hay que dejar que el imán redondo se ubique por sí solo en uno de los extremos del imán rectangular. Así queda listo el dispositivo para el experimento (fig. 2).
Desde la posición final del imán redondo (fig. 3-a) empujamos la tira con los dedos de la mano derecha (suministrándole consecuentemente energía potencial magnética al imán redondo) hasta que el imán redondo se sitúe en la posición inicial en el otro extremo del imán rectangular (fig. 3-b). Luego soltamos la tira y observamos que el imán redondo es movido por una fuerza magnética hasta la posición final describiendo una trayectoria lineal (fig. 3-c). El carril transforma el movimiento giratorio del imán redondo en lineal. Nótese que por no producirse ningún giro no es apropiado seguir refiriéndose a las fuerzas magnéticas de torca propiamente dichas. De aquí en adelante me referiré específicamente a la suma de sus componentes horizontales con el nombre de fuerza magnética por encarrilamiento.
Según la hipótesis propuesta, el sentido de la fuerza magnética por encarrilamiento viene determinado por el sentido de la torca. Por lo tanto, el imán redondo se desplazará de derecha a izquierda cuando la torca tiende a girarlo en el sentido de las manecillas del reloj y de izquierda a derecha cuando la torca tiende a girarlo en contra de las manecillas del reloj. Dicho de una manera más concreta, cuando el polo del imán rectangular sobre el que se apoya la tira de madera es el norte, el imán redondo se desplazará en el sentido que va de su polo sur hacia su polo norte; y, cuando el polo del imán rectangular utilizado cómo carril es el sur, el imán redondo irá en el sentido que va de su polo norte hacia el sur. Esta concordancia de la hipótesis con lo observado constituye la primera prueba a su favor.
Pruebe con los dos polos del imán rectangular y cambiando la polaridad del imán redondo en ambos casos. Si en sus primeros intentos no tiene éxito no se desanime, con un poco de práctica corregirá las pequeñas fallas.
La distancia que separa al imán redondo del grande debe ser la menor posible para aprovechar al máximo la fuerza magnética debida al encarrilamiento que actúa sobre el imán redondo.
Análisis del experimento básico
Tras efectuar con éxito el experimento básico, se despertará en nosotros el interés de comparar los valores de la energía potencial inicial (Ep1i) y de la energía potencial final (Ep1f) del imán pequeño. Así que hagamos los cálculos respectivos.
Ep1i = -m1i B1i cos teta1i
donde,
Ep1i= energía potencial inicial
m1i = momento magnético del imán redondo en la posición inicial
B1i = densidad del flujo magnético en la posición inicial
teta 1i = ángulo entre 180º y 270º
En la posición inicial, la proyección de m tiene sentido opuesto a la dirección de B, por tanto, la fuerza magnética es repulsiva.
Ep1f = -m1f B1f cos teta1f
donde,
Ep1f= energía potencial final
m1f = momento magnético del imán redondo en la posición final
B1f = densidad del flujo magnético en la posición final
teta1f = ángulo entre 270º y 360º
En la posición final, la proyección de m tiene el mismo sentido que la dirección de B, por tanto, la fuerza magnética es atractiva.
Nótese que al tratarse siempre del mismo imán pequeño,
m1i = m1f
Y cómo el campo magnético del imán grande es simétrico,
B1i = B1f
Usualmente de la diferencia entre la energía potencial inicial y final se obtiene el valor del trabajo realizado por una fuerza, pero en este caso no podemos hacer aquello en vista de que el campo magnético cambia de dirección en los extremos del polo del imán grande. En el extremo inicial la fuerza magnética es repulsiva y perpendicular a la fuerza magnética por encarrilamiento; y en el extremo final es atractiva y también perpendicular a la fuerza magnética por encarrilamiento. Esto hace que la energía potencial sobre el extremo inicial tenga signo positivo y sobre el extremo final signo negativo. Debido a que el campo magnético del imán grande forma un ángulo obtuso negativo con el momento magnético del imán pequeño sobre el extremo inicial y un ángulo agudo negativo sobre el extremo final, debemos considerarlo como 2 campos magnéticos distintos. Y puesto que cada campo magnético constituye un sistema de referencia, resulta que estamos utilizando 2 sistemas de referencia en vez de uno solo. Es necesario que haya un único sistema de referencia para estar en condiciones de calcular la variación de la energía potencial entre los extremos del imán grande. Asumiendo como único sistema de referencia la parte del campo magnético sobre el extremo inicial, nos damos cuenta de que el valor de la energía potencial del imán pequeño no cambia,
Ep1f = Ep1i
El significado físico de esta igualdad es que el grado de deformación de las líneas de campo magnético es el mismo tanto en la posición inicial como en la final. Tenga presente que para que la energía potencial magnética se haga cero, la deformación de las líneas de campo magnético debe ser completamente eliminada en la posición final.
Esta igualdad no concuerda con lo que dice la termodinámica. Desde el punto de vista de la termodinámica un sistema de imanes es un sistema no conservativo. A causa de las pérdidas de energía por histéresis, la fuerza magnética no convierte todo el trabajo en energía potencial magnética, ni toda la energía potencial magnética en energía cinética. Lo segundo se expresa matemáticamente diciendo que la variación de la energía potencial magnética entre la posición inicial (extremo izquierdo del imán grande) y la posición final (extremo derecho del imán grande) debió haber sido igual a la energía cinética adquirida por el imán más las pérdidas por histéresis
Ep1i - Ep1f = Ec + pérdidas por histéresis
O sea que la energía cinética debió haber sido inferior a la variación de la energía potencial magnética, pero tenemos que
Ep1i - Ep1f = 0
Puesto que el valor absoluto de la energía potencial final (extremo derecho) es igual a la energía potencial inicial (extremo izquierdo), deduzco que la fuerza magnética por encarrilamiento sigue una trayectoria equipotencial y que consecuentemente T1 constituye un trabajo extra realizado por la fuerza magnética por encarrilamiento. El valor del trabajo extra lo calculamos en base a la fórmula,
T1 = F1 d1
donde,
T1 = trabajo de la fuerza magnética por encarrilamiento con el imán grande 1
F1 = fuerza magnética por encarrilamiento con el imán grande 1
Esta fórmula no es nada fácil de aplicar porque la fuerza magnética por encarrilamiento no tiene un valor constante. Desde la posición inicial hasta la mitad del imán grande parece debilitarse y desde la mitad del imán grande hasta la posición final parece aumentar. No obstante, podemos simplificar el asunto imaginando un valor promedio para utilizarlo en la fórmula.
En conclusión, la fuerza magnética por encarrilamiento (promedio) realizó un trabajo lineal y este trabajo no alteró la cantidad total de energía potencial magnética que le fue suministrada al imán encarrilado.
Según lo observado en el experimento, la energía que debimos haber suministrado al imán pequeño al inicio es igual a la energía potencial final más el trabajo realizado sobre él por la fuerza magnética de encarrilamiento (Ep1f +T1). Sin embargo, la que se suministró era sólo Ep1i, así que hay un déficit de energía igual al valor de T1. Nótese que gastando al inicio una pequeña cantidad de energía para introducir un imán en un campo magnético es posible ocasionar un gran déficit de energía (T1) en el imán pequeño.
La energía negativa no es una energía que tiene un sistema sino por el contrario una energía que no posee un sistema y que por lo tanto se hace cero cuando un agente externo adiciona energía al sistema. El estado de déficit de energía que presenta el imán pequeño lo podemos considerar como un tipo de energía negativa a la que llamaremos energía potencial magnética por encarrilamiento (EPME). El valor del déficit de energía es el máximo en el extremo izquierdo del imán grande y en el extremo derecho es igual a cero. Si bien la EPME se adquiere junto con la energía potencial magnética ordinaria, debe quedar claro que son dos tipos de energía diferentes, puesto que la primera se gasta mientras que la segunda se conserva. Pero, si la EPME es independiente de la energía que le suministramos con la mano al imán pequeño, entonces ¿quién le cede la energía al imán pequeño durante su desplazamiento? Cómo ya se dijo, si el imán pequeño presenta un déficit de energía, únicamente un agente natural fuera de él puede cederle la energía necesaria para que el déficit (o EPME) se haga cero. La EPME en el extremo izquierdo del imán grande se puede expresar así:
Epe1 = (Ep1f+T1) - Ep1f
donde,
Epe1 = energía potencial magnética por encarrilamiento con el imán grande 1
(Ep1f+T1) = energía total que debimos haber suministrado al principio al imán pequeño
Ep1f = energía potencial final del imán pequeño
Eliminando los términos semejantes,
Epe1 = Ep1f - Ep1f + T1
= T1
la fórmula nos dice que fue la energía potencial magnética por encarrilamiento la que se convirtió en el trabajo extra. ¡He aquí un nuevo tipo de energía...! Un imán puede tener al mismo tiempo energía potencial magnética normal y EPME. Una pequeña cantidad de trabajo le permite al imán pequeño adquirir energía potencial magnética y además una gran cantidad de EPME. La EPME disminuye con el desplazamiento al transformarse en trabajo extra y en la posición final se hace cero, aunque las líneas de campo conservan la cantidad de energía potencial ordinaria que tenían en la posición inicial.
Por carecer de los instrumentos de medición necesarios no pude hacer cálculos precisos de los valores de EP1, Ep2 y T1 utilizando las fórmulas de más arriba. Además faltaría calcular el módulo de las fuerzas de torca que actúan sobre el imán pequeño para verificar si, cuantitativamente, la suma de las componentes horizontales de las fuerzas de torca podría ser igual a la fuerza que produce el movimiento lineal. El módulo de las fuerzas de torca se calcula generalmente con la fórmula
M = m B sen teta
donde,
M = módulo de la torca
m = momento magnético del imán
B = densidad del flujo magnético
teta = ángulo entre B y m
A pesar de las carencias mencionadas, ahora por lo menos estamos seguros de que el movimiento del imán encarrilado es un hecho. Pensemos entonces en lo que ocurriría con la energía potencial magnética y el desplazamiento del imán redondo si sustituimos el imán rectangular por otro el doble de largo (fig. 4). Asumiendo que con dicha duplicación la intensidad del campo magnético se incrementa en un 17%, nos damos cuenta que mientras el valor del desplazamiento se duplica, la energía potencial del imán redondo apenas aumenta un 17%.
Ep2i = -m2i B2i cos teta2i
donde,
Ep2i = energía potencial inicial del imán redondo con el imán grande más largo
m2i = m1i
B2i = 1,17 B1i
teta2i = ángulo entre 180º y 270º (muy cercano a teta1i)
Ep2i = -m1i 1,17 B1i cos teta1i
= -1,17 m1i B1i cos teta 1i
= 1,17 Ep1i
Ep2f = -m2f B2f cos teta2f
donde,
Ep2f = energía potencial final del imán redondo con el imán grande más largo
m2f = m1f
B2f = 1,17 B1f
teta2f = originalmente ángulo entre 270º y 360º pero por asunción igual a teta2i
Ep2f = -m1f 1,17B1f cos teta1f
= -1,17 m1f B1f cos teta1f
= 1,17 Ep1f
Ep2i = Ep2f
T2 = F2 d2
donde,
T2 = trabajo de la fuerza magnética por encarrilamiento con el imán grande más largo
F2 = 1,17 F1
d2 = 2d1
T2 = 1,17 F1 2d1
= 2 1,17 F1 d1
= 2,34 T1
El trabajo extra aumentó 2,34 veces mientras que la energía potencial magnética inicial aumentó sólo 1,17 veces. Concluimos que la simple multiplicación de la longitud del imán grande multiplica la producción de trabajo extra y no tanto así el valor de la energía potencial. El aumento de la longitud del imán grande acrecienta el déficit de energía y por lo tanto mayor es la EPME.
Normalmente, el trabajo de una fuerza magnética depende de la distancia que separa a los imanes y esa distancia varía cuando los imanes se desplazan. Con el carril se puede lograr que la distancia entre los imanes no varíe por el desplazamiento del imán encarrilado. El carril impide que la orientación de los imanes cambie y que la distancia entre ellos se haga cero. Debido al encarrilamiento, la distancia deja de constituir una limitación para el trabajo de la fuerza magnética. Dicho trabajo ahora está limitado únicamente por la longitud del imán grande.
Desde el punto de vista de que no sabemos de donde saca el imán redondo el trabajo extra T2, algunos concluirán que el sencillo experimento efectuado viola la ley de conservación de la energía. Pero si analizamos el ciclo completo del experimento mostrado en la fig. 4 veremos que tal violación no existe. El trabajo necesario para llevar el imán redondo de la posición final a la inicial es igual al valor de T2. Recordando que la energía del imán en el extremo izquierdo es Ep2 y no Ep2+T2, resulta que en este caso la energía suministrada con la mano no se acumula sino que se pierde completamente. Sólo una pequeña parte de la pérdida está justificada por el rozamiento, el resto no sabemos cómo se pierde. Además, cómo el valor del trabajo realizado con la mano (que se pierde misteriosamente) es igual al valor del trabajo extra producido (también misteriosamente) por el imán redondo, no hay una producción neta de trabajo extra. La cantidad total de energía del universo no aumenta ni disminuye durante un ciclo de este experimento. El misterio radica principalmente en no saber con certeza a donde va a parar el trabajo suministrado (aquella parte cuya perdida no está justificada por el rozamiento) ni de donde viene el trabajo extra.
Sin embargo, después de haber comprobado el experimento básico, aquella laguna en nuestros conocimientos no nos impide hablar del imán permanente como una posible fuente de energía. Tal como se aprecia en la fig. 5, con un imán rectangular varias veces más largo en vez de retroceder directamente el imán redondo de la posición final B a la inicial A, podríamos primero alejarlo del extremo final del imán rectangular (posición B) en contra de la atracción ejercida por este extremo hasta la posición C, para después retrocederlo por fuera del campo magnético grande de la posición C a la D y por último llevarlo desde la posición D al extremo inicial del imán rectangular (posición A) en contra de la repulsión ejercida por dicho extremo. Rodeando el campo magnético grande seguimos el camino de menor resistencia para el regreso del imán redondo a la posición inicial A. El trabajo total necesario para regresar el imán redondo siguiendo la trayectoria BCDA es inferior al trabajo realizado por la fuerza magnética cuando desplaza al imán redondo de la posición inicial A a la final B. En este ciclo hay una producción neta de trabajo extra. Aunque no se aprecia en la fig. 5, en el tramo AB en el que se deja a la fuerza magnética actuar por sí sola, el imán redondo permanece encarrilado con una regla o una vara en forma de regla. El imán redondo en la posición inicial A tiene energía potencial magnética ordinaria con respecto a la posición D y EPME con respecto a la posición B. El valor de la energía potencial magnética es igual al trabajo necesario para desplazar el imán redondo desde D hasta A, y el valor de la EPME es igual al trabajo necesario para desplazarlo desde B hasta A. El trabajo que realizamos con la mano al desplazar el imán de D hasta A se acumula como energía potencial magnética y puesto que la cantidad de esa energía luego se conserva al desplazarse el imán redondo de A a B, decimos que la que consume el imán redondo hasta hacerse cero es la EPME. Con esta variación del experimento básico sí estaríamos violando la primera ley de la termodinámica... pero por no saber tampoco ahora de dónde sale la energía extra.
Búsqueda de la fuente de energía
Para quitarles la impresión de que me he ido en contra de las leyes de la termodinámica, voy a especular un poco sobre el origen del trabajo extra. Me conformaré con salir del ámbito de lo imposible. Pienso que es falso que las leyes de la termodinámica prohíben la construcción del móvil perpetuo. El error consistió en haber considerado como cerrados a sistemas que en realidad no lo son.
Mi especulación comenzará con la afirmación de que todo el trabajo extra se convierte finalmente en una irradiación de fotones reales (calor) y se concretará en consecuencia a averiguar la ruta más probable que siguieron aquellos fotones.
Suponiendo que tras repetir muchas veces el experimento básico usando siempre los mismos imanes, estos no terminan desgastándose después de extraerles una cantidad de energía igual a la suministrada por el fabricante para su imantación, quedaría claro que los fotones investigados no formaban parte de los átomos de los imanes sino que provinieron de fuera de ellos. Y si suponemos además que el experimento se desarrollaría sin inconvenientes a una temperatura ambiental de 0K, terminaríamos concluyendo que los fotones en cuestión debieron haber sido extraídos del campo de punto cero. Aunque con esta conclusión no entramos en contradicción con la ley de conservación de la energía, ahora toca preguntarse ¿cuál es el mecanismo que permite efectuar aquella extracción sin violar la segunda ley de la termodinámica?
Pensemos en lo que le ocurre a una línea de campo magnético mientras se desplaza el imán encarrilado. Al ser repelida por el polo delantero del imán encarrilado la línea es aplastada cada vez más hasta que súbitamente es atraída por el polo posterior. La línea atraída se une al borde inferior del polo posterior y se contrae, luego sube por el polo posterior alargándose en contra de la atracción que experimenta y finalmente se separa del borde superior del polo posterior. De la descripción hecha concluimos que las líneas de campo magnético propulsan al imán encarrilado únicamente cuando se contraen. Es como si el imán encarrilado después de vencer la fuerza repulsiva del extremo inicial fuese atraído por el extremo final del imán grande. Cuando están en las etapas de repulsión y de alargamiento, las líneas de campo magnético en cambio se oponen al desplazamiento. La fuerza magnética por encarrilamiento es en consecuencia una fuerza de índole atractiva que paradójicamente tiende a alejar al imán encarrilado del grande. Lo concluido es insuficiente para comprender el mecanismo generador de trabajo extra, se hace necesario elaborar una concepción más amplia de la atracción magnética para analizarlo mejor.
Imaginemos dos imanes exactamente iguales, uno libre A y otro fijo B, con los polos norte enfrentados a una distancia "d". A la distancia "d" el imán A se mantiene en equilibrio estático sin ninguna ayuda de nuestra parte. Si con una mano se reduce un poco la distancia "d" acercando el imán A al B y después se suelta el imán A, observaremos que la fuerza de repulsión intenta restablecer la distancia "d" y que el imán A queda casi cómo al inicio. La cantidad de energía con que se desplaza el imán A es igual a la que se le suministró, así que podemos estar seguros de cuál es la fuente de la energía devuelta: nosotros. Ahora volteemos el imán A para que sean los polos opuestos los que esta vez queden enfrentados a la distancia "d". A la distancia "d" no se puede hablar de energía potencial magnética porque al encontrarse los imanes demasiado distantes está roto el sistema de imanes que se atraerían. Osea que otra vez el imán A permanecerá en equilibrio estático por sí solo. Si reducimos lentamente la distancia "d" con la mano acercando el imán A al B, llega un momento en que el imán A es atraído violentamente por el imán fijo B. ¿De dónde salió la energía en el segundo caso? Por la cantidad relativamente grande de la misma, nos damos cuenta de que no salió del trabajo de la mano al desplazar una pequeña distancia el imán A; y cómo el sistema estaba roto al inicio, tampoco puede tratarse de la liberación de una energía potencial acumulada con anterioridad. Profundizando en el asunto, encontramos que el campo magnético del imán B deflecta a los electrones del imán A y que los electrones deflectados atraen electrostáticamente a los núcleos atómicos. La única fuente disponible por lo tanto son las interacciones electrostáticas entre los electrones y los núcleos atómicos.
En los casos comúnmente estudiados en los que actúa la fuerza magnética de atracción, los imanes involucrados terminan juntándose y al volver a separarlos observamos que gastamos la misma cantidad de energía que ellos liberaron al juntarse, nos parece entonces que toda la energía liberada provino de nuestro trabajo. Aquí supondremos en cambio que la energía que gastamos al separar los imanes se pierde de un modo desconocido, o sea que no se acumula en los campos eléctricos de los electrones y núcleos atómicos de aquellos imanes y en consecuencia no es la utilizada por ellos cuando se atraen.
Estamos acostumbrados a ser los responsables de la acumulación de energía en un campo eléctrico, pero no a que una partícula cargada eléctricamente transfiera energía a un campo eléctrico ajeno sin nuestra ayuda. En esta especulación, una partícula cargada eléctricamente tiene la capacidad de transferir por sí sola energía al campo eléctrico de una partícula de signo contrario. Así el sistema de imanes deja de ser para nosotros un sistema aislado porque sabemos que las partículas subatómicas pueden tomar a su vez la energía que dan del campo de punto cero.
Hemos llegado a la pregunta clave en esta especulación: ¿De qué modo una partícula cargada eléctricamente transfiere energía al campo eléctrico de otra partícula sin nuestra intervención? Una partícula libre convierte las ondas del campo de punto cero que le llegan en movimiento vibratorio y este movimiento vibratorio lo transmite a sus propias líneas de campo eléctrico, haciendo que ellas ondulen continuamente. Cada línea de campo eléctrico ondula tal como lo hace una cuerda sacudida de arriba abajo, o sea que presenta amplitud y longitud de onda. Cuando las puntas de un grupo de líneas de campo eléctrico se conectan a otra partícula cargada con electricidad de signo contrario, las dos partículas transmiten energía al grupo de líneas, aunque la partícula externa las hace ondular con mucha mayor amplitud. Las líneas de campo eléctrico ondulan más fácilmente cuando la energía les llega del exterior que cuando les llega del interior. Debido a la transmisión de energía las líneas ondulan cada vez con mayor amplitud. El aumento de la amplitud es una consecuencia de la acumulación de la energía transmitida. El aumento de la amplitud acorta la longitud de onda de las líneas de campo eléctrico. Las líneas ondulantes al perder longitud de onda producen la aproximación de las partículas. La amplitud sólo puede aumentar hasta un valor máximo, a partir del cual ya no se acorta más la longitud de onda y las partículas dejan de aproximarse. Las mismas ondas que en el efecto Casimir empujan directamente las plaquitas, ocasionan indirectamente la atracción eléctrica de las partículas subatómicas. En un espacio absolutamente vacío (sin siquiera ondas del campo de punto cero) no habría efecto Casimir ni atracción eléctrica. O si con un aparato (imaginario por supuesto) generásemos más ondas del mismo tipo que las del campo de punto cero, se incrementarían tanto el efecto Casimir como la atracción eléctrica. Las ondas del campo de punto cero se pueden convertir en atracción eléctrica pero no en repulsión eléctrica. Cuando el grupo de líneas de campo eléctrico se topa con una partícula cargada con electricidad del mismo signo, sus puntas no se unen a ella y consecuentemente no pueden transmitir el movimiento vibratorio de la partícula externa. Sin embargo, si nosotros aproximamos las dos partículas realizando un trabajo, la longitud de onda del grupo de líneas de campo eléctrico se acortará mientras que la amplitud de la ondulación aumentará. Con el aumento de la amplitud se almacena la energía de nuestro trabajo. Al soltar las partículas, la amplitud se reduce y la longitud de onda aumenta. Durante la reducción de la amplitud se libera la energía almacenada (como en el caso de un resorte comprimido que recupera su forma) y esta energía liberada aumenta la longitud de onda de las líneas. Las líneas al aumentar de longitud de onda separan a las partículas. Una vez que la amplitud ha alcanzado el valor mínimo, las partículas dejan de repelerse.
Apliquemos la idea de las líneas ondulantes de campo eléctrico al desplazamiento del imán pequeño a lo largo del imán grande. Cuando acercamos el imán pequeño al extremo inicial del grande, el campo magnético del imán grande deflecta a los electrones orbitales de los átomos del imán pequeño. La fuerza magnética modifica la trayectoria de los electrones orbitales y consecuentemente el momento magnético de estos electrones, pero no mueve el resto del imán. El momento magnético inducido de los electrones y el campo magnético aplicado tienen el mismo sentido y dan origen a una fuerza de atracción, la cual actúa sobre los electrones. La fuerza de atracción ejercida sobre los electrones orbitales, tiende a alejar a los electrones orbitales de sus respectivos núcleos atómicos, ocasionando la tensión de las líneas ondulantes de campo eléctrico que conectan a dichos electrones con los núcleos. Cuando esta tensión se hace muy grande el imán pequeño cede y los núcleos atómicos se ponen en movimiento. Una vez que los núcleos han sido acercados por la fuerza electrostática a sus electrones orbitales, los electrones orbitales se encuentran en capacidad de alejase de los núcleos. Tras el desplazamiento de los electrones orbitales, la fuerza de atracción vuelve a ejercer tensión y el proceso de desplazamiento del imán pequeño se repite. Cómo la fuerza magnética es perpendicular al desplazamiento del imán pequeño no realiza trabajo; es la fuerza electrostática entre los electrones deflectados y los núcleos atómicos la que en realidad mueve el imán pequeño, puesto que ella sí es paralela al desplazamiento del mismo. La reducción de la longitud de onda, ocasionada por el desplazamiento del imán pequeño, aumenta la amplitud de las ondulaciones. La energía requerida para el aumento de la amplitud de las líneas ondulantes de campo eléctrico es aportada por el movimiento vibratorio de los electrones orbitales a las que están conectadas. Nótese que son las propias partículas subatómicas del imán pequeño, y no las del grande, las que le ceden parte de su energía cinética para que se mueva un poco. Al ceder energía cinética obviamente los movimientos de las partículas subatómicas pierden algo de su velocidad. La desaceleración equivale a sufrir un enfriamiento con respecto a la temperatura del campo de punto cero. Gracias a este enfriamiento de las partículas subatómicas, ellas se hacen capaces de absorber fotones virtuales del campo de punto cero. Los partículas subatómicas absorben fotones virtuales hasta que su velocidad de vibración se restablece. El restablecimiento de la velocidad de vibración implica que las partículas subatómicas vuelven a tener la misma temperatura del campo de punto cero. Al equilibrarse la temperatura dejan de absorber fotones virtuales. El desplazamiento parcial del imán pequeño desencadena la absorción de más fotones virtuales y los fotones virtuales recién absorbidos ocasionan un nuevo desplazamiento parcial del imán pequeño. El desplazamiento parcial del imán pequeño y la absorción de fotones virtuales conforman un ciclo que se repite sucesivamente hasta que el imán pequeño llega al extremo final del imán grande.
Vimos que la energía proveniente del campo de punto cero o de nuestro trabajo se acumula en las líneas de campo eléctrico en forma de ondulaciones. La acumulación y liberación de energía en las líneas de campo eléctrico ocurre sin pérdidas. La energía se pierde debido al efecto que produce la fricción sobre la tablita. El efecto de la fricción consiste en hacer que parte de la energía cinética del imán móvil se convierta en el movimiento vibratorio de las partículas constitutivas de la tablita. De las partículas constitutivas de la tablita la energía cinética sale al exterior en forma de calor. Los fotones reales irradiados viajan por algún tiempo hasta ser reabsorbidos por lo que a simple vista nos parece espacio vacío. Para la física el espacio vacío en realidad está ocupado por un entramado de ondas electromagnéticas residuales. Las fluctuaciones del campo electromagnético residual le permiten al espacio vacío emitir y absorber fotones. A diferencia de las fuentes de energía conocidas comúnmente, el campo electromagnético residual al ser precisamente lo que su nombre indica, o sea residual, se recarga una y otra vez inevitablemente. Nos conviene entonces pasar del petróleo del subsuelo al campo electromagnético residual del espacio vacío.
Para verificar que la energía extra proviene del imán pequeño y no del grande, reemplacemos en el experimento básico los imanes permanentes por bobinas recorridas por una corriente continua y monitoreemos con un voltímetro y un amperímetro el consumo de energía eléctrica de las dos bobinas. Si la potencia consumida por la bobina encarrilada aumenta cuando se pone en movimiento y la potencia consumida por la bobina fija no, aquello significaría que efectivamente la energía extra proviene únicamente de la intimidad del imán encarrilado.
El movimiento del imán encarrilado cesa al terminarse las líneas del imán grande que podían unirse al polo posterior. Recordemos que es la contracción de las líneas unidas al borde inferior del polo posterior lo que propulsa al imán encarrilado. El grado de deformación de las líneas de campo no disminuyó por el desplazamiento del imán encarrilado, sino que la deformación se conservó transfiriéndose a los grupos de líneas subsiguientes. Cuando el imán pequeño es regresado con la mano a la posición inicial siguiendo el mismo camino de ida (fig. 3), una parte de la energía aportada con la mano se utiliza para vencer la fricción y, cómo no hay ningún aumento en el grado de deformación de las líneas de campo magnético, deduzco que la energía restante que utilizamos para superar la oposición de la contracción de las líneas de campo magnético, no se almacena en forma de energía potencial magnética ordinaria (a diferencia de la energía suministrada al inicio del experimento que sí se almacenó en aquella forma), pero se almacena en el imán pequeño en forma de energía potencial negativa. A pesar del almacenamiento en forma de energía negativa, es evidente que no hay producción neta de energía extra cuando el imán pequeño sigue un mismo camino de ida y vuelta. Afortunadamente, cómo se observa en la fig. 5, es posible seguir otro camino de regreso para que haya una verdadera producción de energía extra. El camino que el imán pequeño siga al regresar a la posición inicial dependerá del tipo del dispositivo de encarrilamiento utilizado.
Encarrilamiento tubular
Volvamos al carril de la fig. 2 conformado por la regla y el imán grande y tratemos de reemplazarlo por otro aún más simple. Ya que el imán pequeño tiene forma redonda resulta que el más sencillo es un tubo de plástico. Para que el imán pequeño no gire dentro del tubo a causa de su gran diámetro y poca altura, aumentaremos su altura manteniéndolo unido a otro imán de las mismas características. Si acercamos el imán que yace en el tubo al polo del imán rectangular nos llevaremos una desalentadora sorpresa: El imán pequeño no se deplaza como en el experimento básico, la fuerza magnética de torca no produce el movimiento lineal esperado. ¿Cuál es el problema? El tubo le debe quedar un poco holgado al imán para que éste pueda deslizarse en su interior y esa holgura es suficiente para que la fuerza magnética de torca le dé al imán un pequeño giro que lo traba en vez de moverlo linealmente. Hasta el momento hemos visto experimentos realizados con un imán encarrilado sobre el que actúan las fuerzas magnéticas de torca de un solo imán grande. ¿Qué ocurriría si las fuerzas magnéticas de torca de dos imanes grandes actuaran simultánea y opuestamente sobre el mismo imán encarrilado? Aplicando también en este caso la hipótesis de que son las fuerzas magnéticas de torca las que producen el movimiento lineal, deduzco que las fuerzas magnéticas de torca de uno de los imanes grandes neutralizarán el giro de las fuerzas magnéticas de torca del otro imán grande y viceversa, y que las dos fuerzas magnéticas por encarrilamiento resultantes se sumarán al tener igual sentido. Para que el imán pequeño no se trabe dentro del tubo necesitamos por lo tanto un segundo imán rectangular que genere la torca de sentido contrario.
En la fig. 6 apreciamos que el tubo de plástico descansa en un soporte de madera para que el mismo no se mueva lateralmente y para que el centro del imán redondo se encuentre siempre a la misma altura del centro de los imanes rectangulares. Con cada mano agarre un imán rectangular y vaya acercándolos despacio y simultáneamente al imán pequeño (fig. 6-a). Al llegar a cierta distancia comprobará que el imán pequeño es disparado por los dos imanes grandes más allá de sus bordes pero que dos fuerzas magnéticas de atracción terminan acercándolo a los bordes de los imanes grandes (fig. 6-b). El imán pequeño se desplaza a lo largo de la línea central entre los imanes rectangulares. La comprobación de esta nueva aplicación de la hipótesis es otra prueba a favor de la misma.
En el caso de no contar con los imanes rectangulares largos vistos en las figuras 4 y 5, una variante del experimento con el tubo tiene la ventaja de que permite observar directamente la realización del trabajo extra por parte de los imanes rectangulares de la fig. 1 que son de poca longitud. Con este nuevo experimento nos damos cuenta de que la variación de la magnitud de la fuerza magnética por encarrilamiento no significa que no haya producción de trabajo extra. Por eso, fue justamente éste el experimento que a mí, en lo personal, me pareció contundente y me convenció de la realidad del trabajo extra de los imanes permanentes.
Construyamos una cajita alargada con madera de balsa para que sea liviana. Peguemos el imán pequeño (dos imanes pequeños en realidad) en un extremo de la cajita alargada y en el otro extremo un peso pequeño (dos monedas de 1 centavo de dólar estarán bien). Luego, sobre un plano inclinado de madera construyamos un carril con tablitas y triángulos de madera pegados a sus costados para reforzarlo. En su interior se desplazará la cajita que lleva el imán pequeño (los triángulos no se aprecian en la fig. 7). El plano inclinado tiene un ángulo de elevación de 20º y constituye el fondo del carril. La punta posterior del carril está tapada y la anterior destapada. A cada lado del extemo inferior del carril mantengamos inmóvil un imán rectangular, separados uno del otro una distancia de 4 cm. Introduzca la cajita dentro del carril con su tapa posterior topando la tapa posterior del carril, incline la cajita para que quede paralela al plano inclinado y sosténgala con su borde inferior separado una distancia de 1,6 cm del fondo del carril. Esta será la posición inicial A de la cajita. En la posición A el imán pequeño experimenta una fuerza magnética de repulsión dirigida hacia arriba que contrarresta parte del peso de la cajita. Soltamos la cajita desde la posición A y el punto más lejano (que no es exactamente el más elevado) del recorrido de la cajita lo marcamos colocando en él un blanco construido con madera de balsa. Sacamos los imanes rectangulares de los costados, ponemos la cajita otra vez en la posición A y medimos la altura del centro de gravedad de la cajita (h1). Soltamos la cajita y por acción de la gravedad desciende hasta depositarse en el fondo del carril y a continuación la deslizamos con la mano para que choque contra el blanco. La altura h2, que alcanza en este caso el centro de gravedad de la cajita en el momento del impacto, es la altura mínima que debe tener la cajita para golpear el blanco. Siempre que la cajita golpee el blanco podemos estar seguros de que por lo menos alcanzó la altura mínima h2. Volvemos a poner los imanes rectangulares a los costados, soltamos la cajita desde la posición A y observamos que no cae directamente al fondo del carril, sino que mientras cae los dos imanes rectangulares actúan sobre el imán pequeño impulsando la cajita hacia adelante y hacia arriba hasta la posición B. Gracias a que el carril está descubierto en su parte superior, podemos observar que la cajita gira en el plano vertical y que la punta delantera se elevaría mucho si no fuera por los pequeños pesos colocados en ella. Una vez que la cajita alcanza la posición B, el imán pequeño es atraído por los imanes rectangulares y la cajita retrocede depositándose en el fondo del carril y adoptando la posición C. El impacto contra el blanco nos sirve para verificar que la altura h3, que el centro de gravedad de la cajita tiene en la posición B antes de ser atraída, es mayor a la altura h1 que tenía en la posición A. Es innecesario considerar la altura de la cajita en la posición C en este análisis. En la fig. 7 se aprecia que la altura h3 alcanzada durante el impacto es mayor que la altura mínima h2 requerida para el mismo y que la altura mínima h2 es mayor que la altura h1 en la posición inicial. La elevación de la cajita pone en evidencia el trabajo extra de los imanes rectangulares. A causa del rozamiento con el carril, la altura máxima alcanzada por la cajita debería ser mucho menor que la altura h1 en la posición A, pero debido a que la cajita es elevada por los imanes rectangulares hasta la posición B la altura h3 es mayor a la altura h1 que tenía en la posición A. La energía potencial gravitatoria de la cajita en la posición A se convierte en energía cinética, la energía cinética en energía potencial magnética y en EPME, la energía potencial magnética se conserva y la EPME se convierte en trabajo extra, finalmente el trabajo extra se convierte en la energía potencial gravitatoria de la cajita en la posición B.
Si los imanes no aportasen verdaderamente energía a la cajita, la elevarían pero no la dejarían caer. Construyamos otro plano inclinado, esta vez con un mayor ángulo de elevación, por ejemplo 27º. En un dibujo a escala de los imanes podríamos apreciar que la altura máxima alcanzada por el imán pequeño es superior a la que le corresponde en la posición inicial. Cortemos la mayor parte del fondo del carril, sólo deben quedar los primeros 4 centímetros del fondo. Pongamos la cajita en la posición inicial y soltémosla como antes. Observaremos entonces que la cajita cae por la abertura rectangular después de haber sido elevada por los imanes. La fuerza magnética impulsora es mayor que el peso de la cajita (por eso la cajita se eleva) y sin embargo no le impide caer. Hay que tener cuidado de que la cajita no se apoye en nada durante su caída porque eso interrumpiría la caída. Debido a que las superficies en contacto varían aleatoriamente en magnitud de un lanzamiento de la cajita a otro, el valor de la fricción entre las superficies es irregular y eso hace a su vez que los resultados no sean siempre iguales.
El trabajo extra también se verifica repitiendo el experimento en forma cíclica con el ángulo de elevación de 20º e imanes grandes de por lo menos 15 cm de largo. Justo en el instante en que el imán pequeño se detiene después de haber sido impulsado por los imanes grandes, tomamos rápidamente la cajita con una mano, abrimos las dos puertas iguales que componen una rampa, elevamos la cajita verticalmente una distancia ligeramente inferior a la altura a la que previamente fue alzada por los imanes grandes, cerramos las puertas de la rampa, dejamos que resbale la cajita, abrimos las puertas de la rampa y la cajita cae pasando por la posición inicial. Nótese que en este ciclo imaginario la mano levanta menos que los imanes grandes. Entre más largos sean los imanes grandes, mayor es la altura alcanzada por la cajita y consecuentemente aumenta el límite al que se la puede elevar con la mano.
Los dos mecanismos anteriores se podrían automatizar para facilitar su estudio reemplazando el imán pequeño por una bobina circular, así en vez de acercar y separar los dos imanes grandes, o de subir y bajar el imán pequeño, la puesta en marcha del mecanismo sólo sería cuestión de prender y apagar la bobina. El sentido del desplazamiento de la bobina cambiaría según los cambios de polaridad de la bobina producidos por una corriente alterna (revise la explicación dada casi al final del subtítulo "Experimento básico"). Además se podría controlar la potencia de la bobina variando la intensidad de la corriente alterna.
Para que el motor lineal de la fig. 8 sea eficiente, el campo magnético de los imanes permanentes debe ser muy fuerte y el campo magnético de la bobina por el contrario muy débil, de este modo el consumo de energía eléctrica de la bobina se reduce lo más posible. Pero, cómo la energía extra provenía del imán pequeño y éste fue reemplazado por la bobina, la eficiencia siempre será inferior al 100%. Por no tener la misma composición química de un imán permanente una bobina no adquiere EPME. En la bobina las cargas positivas que participan en la atracción eléctrica que impulsa a los electrones de la corriente son producidas artificialmente por una fuente de fuerza electromotriz. La bobina extrae todo el tiempo la energía de la fuente de fuerza electromotriz. Sin embargo, el motor lineal de la fig. 8 al funcionar tan sólo con dos imanes tiene la ventaja de ser muy compacto.
Consideremos por separado la acción de cada imán sobre la bobina circular. La bobina queda entonces dividida en dos partes, mitad izquierda y mitad derecha. En cada mitad el campo magnético del imán, la corriente y las fuerzas de Lorentz son perpendiculares entre sí. Y puesto que en la mitad izquierda de la bobina, el sentido del campo magnético del imán y de la corriente son contrarios a los de la mitad derecha, concluimos que las fuerzas de Lorentz que actúan en las mitades de la bobina tienen el mismo sentido. Si a continuación determinamos con la regla de Ampère el sentido del campo magnético de la bobina para conocer la ubicación de los polos norte y sur de esta, comprobaremos que las fuerzas que experimenta la bobina tienden a moverla linealmente.
Multiplicando la fuerza magnética neta que actúa sobre la bobina por la longitud de los imanes grandes obtenemos el trabajo que realiza aquella fuerza. Si la bobina fuera rectangular la fuerza sobre un tramo rectilíneo de conductor seríaF = L I B sen teta
donde,
F = fuerza que desplaza al tramo de conductor
L = longitud del tramo de conductor
I = intensidad de corriente
B = densidad del flujo magnético
teta = ángulo entre el campo magnético B y la intensidad de corriente I
Para calcular la energía potencial magnética se necesita conocer el momento magnético de la bobina. El módulo del momento magnético de una espira se define cómo
m = I A
donde,
m = momento magnético de la espira
I = intensidad de corriente
A = área de la espira
Aunque lo más probable es que el valor de la fuerza impulsora varíe a lo largo de su recorrido, ya que el valor de la fuerza magnética por encarrilamiento del imán permanente pequeño no es constante, el cálculo del trabajo que ella realiza y el cálculo de la energía potencial magnética en las posiciones inicial y final siempre serán menos engorrosos con una bobina que con un imán permanente.
Recordemos la fórmula de la torca sobre una bobina rectangular
torca = 2 F a sen teta
donde,
F = fuerza experimentada por los conductores
a = mitad de la anchura de la bobina rectangular
teta = ángulo entre el campo magnético B y la perpendicular al plano de la bobina rectangular
Puesto que tanto la fuerza que produce el desplazamiento de la bobina en el motor lineal de la fig. 8 como la que produce la torca sobre la bobina rectangular tienen su origen en la transmisión de la energía cinética de los electrones deflectados por el campo magnético al conductor, llegamos a la conclusión de que ambas fuerzas son la misma. Esto está en concordancia con lo expresado respecto a la producción de movimiento lineal por parte de las fuerzas magnéticas de torca de los imanes permanentes. O sea que la fuerza que impulsa la bobina en el motor lineal de la fig 8 vendría a ser el equivalente a la fuerza magnética por encarrilamiento de los imanes permanentes.
Encarrilamiento con brazo de palanca
Puesto que la deformación de las líneas de campo magnético del experimento básico no cambiaría gran cosa si el imán pequeño no siguiese una trayectoria perfectamente rectilínea, podemos probar dispositivos de encarrilamiento diferentes al de la fig. 2 en cuanto a la trayectoria del imán pequeño para determinar si también con ellos obtenemos energía extra. En cada uno de los casos en que variemos ligeramente la trayectoria descrita por el imán pequeño habrá que determinar además la cantidad de energía extra que el mismo pierde o gana.
Utilicemos un dispositivo giratorio para convertir el movimiento lineal en uno ligeramente curvo y luego trataremos de convertir ese movimiento curvilíneo en un movimiento circular.
Cómo en la fig. 9 el imán pequeño está fijo a uno de los extremos de una vara y el otro extremo de la vara está sujeto a un eje, cuando el imán pequeño está en movimiento traza una línea en forma de arco. Con el brazo de palanca de la fig. 9 se pretende que el imán pequeño describa una trayectoria lo menos arqueada posible. En la fig. 9-a el imán encarrilado es mantenido inmóvil en la posición inicial con una mano. Luego es soltado y describe el arco. La flecha indica la torca derivada de la fuerza magnética por encarrilamiento. En la fig. 9-b el imán encarrilado llega al otro extremo del imán grande y se detiene. En la posición final lo que mantiene inmóvil al imán encarrilado es una fuerza magnética de atracción.
Ya que debemos llevar al imán encarrilado más allá de la posición final es indispensable averiguar la cantidad de energía que se requiere para liberarlo de la fuerza magnética de atracción, o más concretamente, el número de imanes pequeños y grandes necesarios para tal propósito. Al salir del campo magnético del imán grande, el imán encarrilado experimenta una fuerza magnética de atracción que tiene sentido contrario a la fuerza magnética por encarrilamiento.
Según parece, la intensidad de la fuerza opuesta de atracción, sumada a la inercia y a la fuerza de rozamiento, superan a la intensidad de la fuerza magnética por encarrilamiento. En la fig. 10 asumo que son necesarios 3 imanes pequeños impulsados cada uno por un imán grande.
Cuando el imán encarrilado está entrando en el campo magnético del imán grande, antes de llegar a la posición inicial, actúa en cambio sobre él una fuerza magnética de repulsión que le impide entrar en el campo magnético del imán grande. Esta fuerza magnética de repulsión también tiene sentido contrario a la fuerza magnética por encarrilamiento. Asumo que las intensidades de las fuerzas de atracción y repulsión son iguales, y que también son iguales la inercia y la fuerza de rozamiento. Por eso, en la fig. 11 utilizo también 3 imanes pequeños impulsados cada uno por un imán grande para superar la oposición de la fuerza magnética de repulsión.
Los imanes pequeños se encuentran inmóviles en las posiciones indicadas en las figuras 10 y 11 antes de partir.
Aún con los imanes rectangulares de poca longitud de la fig. 1. es posible experimentar haciendo saltar un imán pequeño desde el extremo de un imán rectangular donde es atraído hacia el extremo de otro imán rectangular, el cual lo repele. Para que el salto pueda darse, bastaría colocar en la fig. 10 otro imán rectangular junto al imán rectangular que atrae al imán impulsado a una distancia menor a la longitud del desplazamiento de los imanes impulsores (fig. 12).
Veamos si basándonos en el experimento de la fig. 12 podemos diseñar un motor. Primero consigamos 8 imanes rectangulares mucho más largos y además un poco más anchos que los de la fig. 12, y conformemos con ellos un octágono separándolos unos de los otros siempre a igual distancia. Con imanes estáticos bastante largos logramos que el trabajo total de la fuerza magnética de torca encarrilada supere a la energía total requerida para vencer las fuerzas opuestas de repulsión y de atracción que se presentan a la entrada y a la salida de los imanes estáticos respectivamente. Sobre 7 de los 8 imanes largos coloquemos 7 imanes pequeños, uno sobre cada imán largo y en forma desfasada, esto es que las posiciones ocupadas por los imanes pequeños sobre sus respectivos imanes largos sean diferentes. Para determinar con precisión las posiciones de los imanes pequeños, dibuje en una hoja de papel primero uno de los imanes largos, después dentro de él dibuje la trayectoria ligeramente curva que describen los imanes pequeños y finalmente sobre aquella trayectoria dibuje los 7 imanes pequeños repartiéndolos a intervalos regulares. El primer imán pequeño debe estar junto al borde inicial del imán largo y el último junto al borde final. La distancia que separa a los 7 imanes pequeños dibujados debe ser un poco mayor que la distancia que separa a los imanes grandes. Las posiciones que los imanes pequeños ocupan en el imán largo dibujado son las mismas que ocuparán en los 7 imanes largos del motor. En la fig. 12 podemos apreciar como debe quedar el desfase de los imanes pequeños. Con ese desfase se pretende conseguir que cada vez que uno de los imanes pequeños enfrentase una fuerza opuesta a la entrada o salida del campo magnético de alguno de los imanes largos, hayan en ese instante 6 imanes pequeños sumunistrándole energía cinética a aquel imán pequeño. Cuando la energía cinética vence la fuerza opuesta de repulsión se convierte en energía potencial magnética y en EPME, la energía potencial magnética se conserva y la EPME se convierte en trabajo extra. Cuando la energía cinética vence la fuerza opuesta de atracción, la energía potencial magnética se hace cero.
¿La torca de los imanes se ha convertido en movimiento perpetuo? Puesto que se obtuvo teóricamente trabajo extra, antes de catalogar de absurdo al dispositivo imaginario de la fig. 13 sería mejor, por prudencia, construirlo y experimentar con él para averiguar si en verdad se produce algún efecto no previsto que se oponga al movimiento y que sea imposible de remediar. Será indispensable definir correctamente el inconveniente que se presente. Por ejemplo, aunque los imanes se comporten como fuentes de energía este hecho pasaría inadvertido si la energía que proporcionan no es suficiente para poner en movimiento el dispositivo. Esto, bien comprendido, no eliminaría la posibilidad de movimiento perpetuo.
Una prueba que está al alcance de todos nosotros consiste en analizar si el imán impulsado puede o no pasar del extremo final al extremo inicial del siguiente imán estático. En vista de que estamos seguros del funcionamiento del brazo de la fig. 9, y de que el motor de la fig. 13 está basado en el funcionamiento de aquel brazo, concentrémonos en un brazo del motor de la fig. 13 y pensemos que si este brazo se mueve del mismo modo que el de la fig. 9 los demás brazos deben también hacerlo y que ese movimiento les da energía cinética para sacar al primer brazo del imán estático (cómo en el caso de fig. 10) y meterlo en el imán estático siguiente (cómo en el caso de la fig. 11). Un solo salto es suficiente para demostrar la viabilidad del motor. Después del salto del primer brazo de un imán estático al siguiente nada hace suponer en este primer análisis que los demás brazos no podrán saltar sucesivamente.
De lo que ya podemos estar seguros es que el momento de la fuerza magnética de atracción produce en el eje mucha fricción y que si no acercamos lo suficiente los imanes móviles a los estáticos esa fricción excesiva, combinada con el debilitamiento de la fuerza magnética impulsora en la parte media de los imanes estáticos, impedirán que el motor de la fig. 13 gire.
Si los imanes pequeños estuvieran en fase, es decir, ocupando las mismas posiciones sobre sus respectivos imanes estáticos (como los imanes impulsores de las figuras 10 y 11) y el número de ellos fuera par (en este caso conviene uno por cada imán estático, o sea, 8 imanes pequeños), el momento de la atracción ejercida sobre cualquiera de los imanes pequeños sería contrarrestado por el momento de la atracción ejercida sobre el imán pequeño del respectivo extremo opuesto del motor. De este modo la fricción dejaría de constituir un grave obstáculo. Sin embargo, es fácil darse cuenta de que cuando todos los imanes pequeños son atraídos o repelidos al mismo tiempo el motor no puede moverse. Desde el siglo XIII la humanidad viene buscando el modo de que los imanes giren continuamente sin ninguna ayuda externa pero, de acuerdo con lo que hemos visto, aquella no debió haber sido la idea fundamental. La idea fundamental debió haber sido la realización de un trabajo para extraer energía de los imanes permanentes. Si queremos extraer energía de los imanes pequeños en fase necesitamos conectar al eje un motor eléctrico (fig. 14). El motor eléctrico se activaría sólo cuando los imanes pequeños necesiten pasar de un imán estático al siguiente y el suministro de energía eléctrica se cortaría cada vez que entren en acción las fuerzas magnéticas por encarrilamiento. Así los imanes y el motor eléctrico propulsan al eje alternativamente. Los imanes lo hacen rápidamente y el motor lentamente. Después de cada intervención de los imanes y del motor hay una pequeña pausa. El motor eléctrico al ser impulsado por los imanes se comporta como un generador. La energía eléctrica producida por el motor eléctrico se almacena en una batería. La energía eléctrica suministrada intermitentemente al motor eléctrico proviene de la batería. La energía sobrante de la batería podría destinarse a otros fines.
A los dispositivos de las figuras 13 y 14 los podríamos llamar motores epméticos.
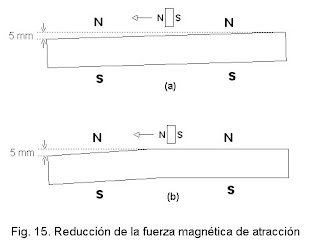Para reducir el efecto de frenado que sufre la rueda cuando el imán pequeño sale del campo magnético del imán estático, es conveniente debilitar la fuerza magnética de atracción, causante del efecto de frenado, aumentando la distancia entre el imán pequeño y el extremo final del imán estático. Con un incremento de 5 mm la fuerza magnética de atracción deja de constituir un obstáculo insalvable para el imán pequeño durante su salida. En la fig. 15-a el imán grande descansa inclinado con el propósito de que la separación entre los imanes vaya en aumento a medida que el imán pequeño avanza, pero eso hace que disminuya mucho la intensidad de la fuerza magnética impulsora y consecuentemente el trabajo que esta fuerza realiza. En la fig. 15-b se optó por doblar ligeramente el imán grande para minimizar lo más posible la pérdida del trabajo de la fuerza magnética impulsora.
Con los motores eléctricos rotatorios estamos acostumbrados a que una fuerza de torca gire directamente el rotor. Por eso conviene notar que en los dos motores propuestos, el giro de los imanes pequeños tal cual es normalmente no forma parte del movimiento circular de los brazos sino que se convierte en un movimiento curvo lo más lineal posible para que sea ese movimiento casi lineal el que conforme el movimiento circular. Suena contradictorio, pero para que la torca de los imanes permanentes pueda mover un eje antes la rotación que produce debe convertirse en un movimiento casi lineal.
Un sistema de generación pequeño, de eficiencia superior al 100% y capaz de alimentar las 24 al día a una batería sería un gran incentivo para el uso masivo del automóvil eléctrico porque le permitiría a este tipo de vehículo independizarse de la red eléctrica.
A continuación realizaremos experimentos relacionados con el incremento de la fuerza magnética por encarrilamiento, su cambio de sentido y la generación de la misma porque analizando los factores que intervienen en cada caso podríamos comprender más concienzudamente el funcionamiento de los dispositivos de las figuras 13 y14.
Incremento de la fuerza magnética por encarrilamiento
El dispositivo de la fig. 16 consta de dos imanes redondos de neodimio de 4,8 mm de diámetro y un imán rectangular de ferrita de 47,6 mm x 22,2 mm x 9,5 mm. En la disposición mostrada el imán superior de neodimio es atraído y mantenido en esa posición por el extremo correspondiente del imán rectangular y sobre el imán inferior de neodimio actúa la fuerza magnética por encarrilamiento que en cambio tiende a subirlo. Cómo la fuerza de atracción supera a la fuerza magnética por encarrilamiento el dispositivo permanece inmóvil.
Desplacemos el imán rectangular en línea recta, de arriba a abajo y de abajo a arriba. Los movimientos del imán rectangular no deben tener mucha velocidad para permitir que los imanes de neodimio puedan seguirlos. No obstante, al cabo de algunas oscilaciones del imán rectangular observaremos que los imanes de neodimio oscilan más rápido que el imán rectangular. La velocidad de oscilación de los imanes de neodimio va en aumento hasta que la amplitud de la oscilación es la suficiente para permitir que estos se liberen de la atracción ejercida por el imán rectangular y entonces salen disparados cómo se muestra en la fig. 17. Sorprende el ver cómo los imanes de la rueda se mueven por su propia cuenta.
La acumulación de energía potencial magnética ordinaria por parte de los imanes de neodimio no explica este fenómeno, pues, cómo se aprecia al principio de las oscilaciones, a los imanes de neodimio les es posible seguir los movimientos del imán rectangular sin ningún inconveniente y consecuentemente no debería acumularse la energía que aportamos con la mano.
Pienso que el aumento de la velocidad de las oscilaciones de los imanes de neodimio es producido por el aumento intermitente y continuo de la intensidad de la fuerza magnética por encarrilamiento. Cada vez que la fuerza magnética por encarrilamiento aumenta sube un poco más rápido al imán inferior de neodimio y, cuando disminuye, la atracción ejercida sobre el imán superior de neodimio baja este imán a la posición inicial. Puesto que se trata de un proceso que se intensifica con el transcurso del tiempo, la fuerza magnética por encarrilamiento finalmente suministra a los radios la velocidad necesaria para que los imanes de neodimio salgan lejos de la influencia del imán rectangular.
Alternancia del sentido de la fuerza magnética por encarrilamiento
Tome dos imanes rectangulares y métalos en una cajita de madera. La separación entre ellos es de 1 mm. Es conveniente utilizar tablas de 4 mm de grosor para la construcción de la cajita (fig. 18-a).
Encima de la cajita va una rueda de madera de 4 radios. Los extremos de los radios llevan 4 imanes redondos de ferrita, uno por cada radio. El contorno de la rueda no debe rebasar el perímetro de los imanes rectangulares, lo adecuado es que quede dentro de ese perímetro (fig. 18-b).
Una vez armado todo el dispositivo (fig. 19) veremos que la rueda permanece inmóvil, cómo si ninguna fuerza magnética actuase sobre los imanes de la misma.
Pero si movemos un poco la rueda con un dedo, digamos unos 5 mm, en uno y otro sentido, notaremos la presencia de una fuerza magnética que la hace regresar a su situación inicial cuando la soltamos. Dando una vuelta completa a la rueda se obtiene el esquema de las torcas de la fig. 20, en el que observamos que el sentido de la fuerza magnética por encarrilamiento que les da origen se invierte en forma regular. La posición final de cada imán pequeño coincide con la posición inicial del imán pequeño que lo antecede. La vuelta se la realiza despacio y pausadamente, dejando que la respectiva fuerza magnética por encarrilamiento haga su trabajo. Con más vueltas constataremos que el esquema de la fig. 20 se mantiene igual en todas las vueltas.
Si el dispositivo fuera de mayores dimensiones le podríamos añadir a cada radio una bisagra (fig. 21) con el propósito de que cada vez que los imanes redondos tengan que enfrentar una fuerza magnética por encarrilamiento opuesta al giro de la rueda, los imanes redondos en vez de chocar directamente contra ella se eleven por efecto de la misma. De este modo disminuye la cantidad de energía necesaria para girar la rueda, porque ya no se tendría que vencer directamente la fuerza magnética por encarrilamiento de sentido opuesto sino solamente elevar los imanes y la parte elevable de los radios. Al eje le llega tan solo la porción del peso que se apoya en la bisagra (la otra porción es contrarrestada por la fuerza magnética de repulsión) y esta reducción de la carga que debe soportar el eje le permite girar con más facilidad. Una vez que la fuerza magnética por encarrilamiento deja de tener sentido opuesto, los imanes y la parte elevable de los radios caen a causa de su propio peso y la parte elevable vuelve a formar un ángulo de 180º con la parte no elevable. A la rueda con bisagras de la fig. 21 se le podría extraer energía con un motor tal cómo se hizo en el caso de fig. 14. El motor eléctrico se prendería cada vez que la fuerza magnética por encarrilamiento tenga sentido opuesto al giro de la rueda y se apagaría cada vez que la fuerza magnética por encarrilamiento tenga el mismo sentido que el giro de la rueda.
Nótese que los radios de los dispositivos de las figuras 13 y 14 también pueden llevar bisagras. En ambos dispositivos las bisagras servirían para reducir el efecto de frenado que la fuerza magnética de repulsión ejerce sobre cada imán pequeño mediante la elevación de los imanes pequeños. La caída de un imán pequeño ocurre inmediatamente después de que el mismo ha entrado en el campo magnético del imán grande.
Generación de una fuerza magnética por encarrilamiento
Para el experimento siguiente se necesitan 3 imanes de ferrita en forma de anillo de 2,85 cm de diámetro, los cuales se apilan conformando un único imán.
Consigamos 2 tiritas de madera de balsa, una de 28 x 1 x 0,5 cm y otra de 12 x 1 x 0,5 cm. Con un clavo de 5 cm de longitud perforemos el centro de la tirita corta, asegurándonos de que el clavo quede holgado para que sirva de eje. Introduzcamos el clavo en la tirita larga, a 2 cm del borde final. El clavo debe quedar apretado esta vez. El otro extremo de la tirita larga nos servirá de mango.
Juntemos 2 imanes redondos de neodimio de 4,8 mm de diámetro, coloquemos el par de imanes en la tirita corta a 4 cm del clavo y sujetémoslos a ella envolviendo con cinta adhesiva los imanes de neodimio y la tirita. De aquí en adelante consideraremos el par de imanes de neodimio como uno solo.
Tomemos con una mano el mango del dispositivo y mantengamos la tirita corta encima de la pila de imanes en forma de anillo, aproximadamente a 2 cm de ella. El imán de neodimio lo colocaremos en todas las posiciones posibles, verificando si en alguna posición es desplazado por una fuerza magnética. Al hacer lo dicho constataremos que el imán de neodimio nunca es desplazado. Con la pila de imanes en forma de anillo y el imán de neodimio en esta disposición debería actuar una fuerza magnética por encarrilamiento sobre el imán de neodimio, pero por alguna razón no es así. Únicamente moviendo circularmente el clavo alrededor del centro del polo superior de la pila de imanes comenzará a actuar una fuerza magnética por encarrilamiento sobre el imán de neodimio. En realidad se deben producir dos movimientos al mismo tiempo: el movimiento circular del clavo y el giro del imán de neodimio alrededor del clavo. El primer movimiento debe ser capaz de mantener el segundo.
Practiquemos primero los dos movimientos del imán de neodimio sin utilizar la pila de imanes. El objetivo es lograr que el imán de neodimio se mantenga girando en torno al clavo. Para que el imán de neodimio gire continuamente, haremos que el clavo, en posición vertical, describa círculos de 4 cm de diámetro. No es aconsejable comenzar el movimiento de traslación del clavo desde una situación de inmovilidad de la tirita corta, así que antes de comenzar a mover circularmente el clavo con una mano pondremos a girar el imán de neodimio alrededor del clavo impulsándolo con un dedo de la otra mano. En la fig. 22 se aprecia que el clavo y el imán de neodimio se mueven en el mismo sentido; en este caso, en contra de las manecillas del reloj.
Logrado el objetivo llevaremos el clavo, sin dejar de moverlo circularmente, sobre la pila de imanes y lo bajaremos hasta que quede dando vueltas a 2 cm de altura con respecto a ella (fig. 23). A medida que descendemos el clavo, el radio de su movimiento se va reduciendo. En este segundo paso el clavo nunca sale del perímetro de los imanes en forma de anillo. El diámetro de los círculos descritos por el clavo debe ser de 1,8 cm aproximadamente. Cuando el imán de neodimio gira en el sentido que va del polo norte al sur, el polo de la pila de imanes que debe estar arriba es el norte. Y cuando gira de sur a norte, el polo que debe estar arriba es el sur.
Una vez que el clavo se encuentre girando a 2 cm por encima del polo superior de la pila de imanes, notaremos que el imán de neodimio gira con más facilidad que cuando estaba a mayor altitud con respecto a ella. Al parecer, se genera una fuerza magnética por encarrilamiento y esta fuerza generada contribuye al giro del imán de neodimio.
Volteemos la pila de imanes para cambiar de polo superior y tratemos de girar el imán de neodimio tal como lo hicimos anteriormente. En esta ocasión no lo lograremos. La fuerza magnética por encarrilamiento que antes nos ayudó a girar al imán de neodimio ahora tiene sentido contrario e impide el giro.
Si reemplazamos la pila de imanes en forma de anillo por un imán de mayor diámetro, digamos 11 cm, y sin el agujero central podríamos tratar de realizar el mismo experimento con la única diferencia de que el imán de neodimio ya no giraría por fuera del perímetro del imán fijo sino que giraría dentro de dicho perímetro (fig. 24).
Lo especial de la fuerza magnética por encarrilamiento generada con el trabajo de un agente externo es que su acción es continua, o sea que no se interrumpe como ocurre con la fuerza magnética por encarrilamiento que vimos anteriormente.
Motor epmético con bisagras e imanes inclinados
Cómo técnicamente es muy complicado armar un octágono con 8 imanes inclinados debido a que las fuerzas que los imanes ejercen entre sí son muy intensas, aunque las dimensiones de los mismos no sean tan grandes como las de los que se aprecian en las figuras 13 y 14, decidí quitarle 4 imanes al octágono para suprimir la interacción entre los imanes que lo conforman. Posteriormente me dí cuenta de que el nuevo diseño podía prescindir de 2 imanes más, con lo cual se simplificaría mucho la construcción sin cambiar el funcionamiento. Así surgió el diseño del prototipo de motor epmético en fase que a continuación estudiaremos, el cual incorpora bisagras y la inclinación de los imanes grandes. Los materiales que utilicé en su construcción son: 2 imanes rectangulares de ferrita de 47,6 mm x 22,2 mm x 9,5 mm, 2 imanes redondos de neodimio de 4,8 mm de diámetro, plywood de 6 mm, madera de balsa de 2,5 mm, masilla epóxica, 3 clavos, tela, hilo, 2 tapas enroscables de bebidas gaseosas y monedas de un centavo de dólar estadounidense.
Cómo todo motor el prototipo consta de dos partes principales: el estator y el rotor.
El estator está hecho casi en su totalidad de plywood. El estator comprende una tabla de plywood sobre la cual se pegaron el soporte del rotor, dos soportes para imán grande y dos soportes para polea. El soporte del rotor está perforado verticalmente en el centro. En la cabecera de los soportes para imán grande pegué un rectángulo de madera de balsa de 5 mm de alto para inclinar el imán grande y al pie pegué un rectángulo de 2,5 mm de altura para impedir que el imán grande resbale. Ambas poleas de los soportes tienen dos canales. Los 4 canales tienen el mismo diámetro. Éstas poleas están hechas de masilla epóxica modelada alrededor de un clavo.
El rotor consta básicamente de una tablita de madera de balsa dividida en tres partes: una media y dos laterales o brazos. El centro de la parte media se encuentra atravesado por un clavo, el cual fijé con masilla epóxica. A la masilla epóxica también le dí la forma de una polea de dos canales. Los canales tienen igual diámetro. El clavo se introduce en el agujero del soporte. Cada brazo está unido a la parte media mediante un cuadradito de tela que pegué por encima de la juntura. Los cuadraditos de tela son las bisagras. Una tablita pegada en la parte media, por debajo de cada cuadradito de tela, impide que los brazos desciendan excesivamente. En cada extremo de los brazos va pegado por debajo un imán redondo de neodimio y por encima dos monedas que sirven de pesos para que los imanes de neodimio no se eleven en exceso.
Alrededor de cada canal de la polea del rotor enrollamos un hilo. Los hilos se enrollan en sentidos contrarios para que al desenrollarse giren el rotor en un mismo sentido. Los extremos libres de los hilos se llevan hasta los respectivos canales de las poleas de los soportes. De cada hilo cuelga un tapita. Sin los imanes grandes puestos en sus soportes, el rotor se pone en movimiento depositando 6 monedas en cada tapita. Una tapita tiene una masa de 2,68 g y una moneda una masa de 2,52 g, así que
peso de una tapita = (0,00268 kg) (9,8 m/s^2)
= 0,0263 N
peso de una moneda = (0,00252 kg) (9,8 m/s^2)
= 0,0247 N
Cómo ya dije el funcionamiento del prototipo es similar al del motor epmético de la fig. 14. El rotor requiere ser movido con un par de fuerzas alto y una velocidad angular baja. A velocidad baja, el rotor es frenado débilmente por las fuerzas de repulsión y cuando las fuerzas magnéticas por encarrilamiento terminan de acelerar el rotor, éste alcanza una velocidad superior a la que tenía antes de comenzar a ser desacelerado. Los imanes pequeños salen de los campos magnéticos de los grandes con mayor velocidad que la que tenían justo antes de entrar. Cuando el rotor es girado continuamente con un par de fuerzas bajo y una velocidad angular alta, el rotor deja de producir trabajo extra neto y pasa a ser un consumidor de energía. A velocidad alta, el rotor es frenado bruscamente por las fuerzas de repulsión y cuando las fuerzas magnéticas por encarrilamiento terminan de acelerar el rotor, éste no alcanza la velocidad que tenía antes de comenzar a ser desacelerado. Los imanes pequeños salen de los campos magnéticos de los grandes con una velocidad menor a la que tenían justo antes de entrar. Puesto que con el sistema de pesos y poleas no podemos alcanzar el par alto y la velocidad baja debido al diámetro demasiado pequeño de la polea del rotor, el sistema de pesos y poleas no puede hacer el papel de motor eléctrico. Así que empujaremos nosotros mismos el rotor con una mano.
Para minimizar el efecto de frenado de las fuerzas de repulsión no solo vamos a recurrir a la velocidad de giro baja sino que además recurriremos al empleo de bisagras. Con el propósito de probar las bisagras y el declive de los imanes grandes en forma combinada, observemos que tan lejos las fuerzas magnéticas de torca pueden impulsar el rotor. Coloquemos los imanes grandes en los soportes en los que permanecerán en posición inclinada. Los hilos se enrollan en los canales de la polea del rotor retirando los imanes grandes de los soportes, girando la parte media del rotor con la mano y volviendo a colocar los imanes grandes en los soportes. En cada tapita deben haber 5 monedas, las cuales sirven para compensar la oposición que ofrece la fricción al movimiento. Los imanes pequeños se encuentran inicialmente fuera de los campos magnéticos de los grandes. Empujamos el rotor lentamente aplicando la fuerza en su parte media. Debemos tener claro las tres fuerzas magnéticas que deben actuar consecutivamente sobre los imanes pequeños: la primera fuerza en manifestarse es la de repulsión, la segunda es la fuerza magnética por encarrilamiento y la tercera la fuerza de atracción. Las fuerzas de repulsión y atracción tienen sentido opuesto a la fuerza magnética por encarrilamiento y por lo tanto se oponen al movimiento. La primera reacción de los imanes pequeños al acercarse a los grandes es elevarse. Los imanes pequeños se elevan alrededor de 7 mm. Con la elevación de los imanes pequeños constatamos el buen funcionamiento de las bisagras, o sea que a los imanes pequeños les resulta más fácil elevarse que confrontar directamente a las fuerzas de repulsión. Al continuar con el empuje del rotor, observamos que llega un momento en el que los imanes pequeños descienden y son impulsados por las fuerzas magnéticas por encarrilamiento. La atracción magnética que sufren los imanes pequeños en los extremos finales de los grandes no los atrapa e inmoviliza. El alejamiento de los imanes pequeños de los extremos finales demuestra que el declive de los imanes grandes sirvió para debilitar la fuerza magnética de atracción propia de aquellos extremos. Los imanes pequeños se detienen a pocos centímetros de los extremos iniciales de los otros imanes grandes. Empujamos nuevamente el rotor y los imanes pequeños son impulsados otra vez por las fuerzas magnéticas por encarrilamiento completando una vuelta. Hasta aquí podemos decir que tanto las bisagras como el declive de los imanes grandes han funcionado tal como se esperaba en la primera prueba.
Si pusiéramos 12 monedas en cada tapita y aumentáramos 6 veces el diámetro de la polea del rotor para que el mismo gire muy despacio sin imanes grandes, el prototipo sería un móvil perpetuo rudimentario porque luego con los imanes grandes el rotor giraría más rápido. Tenga presente que cualquier sistema de imanes es un sistema no conservativo y que de acuerdo con esto el rotor debe girar siempre más despacio con los imanes grandes que sin ellos.
Una alternativa al agrandamiento de la polea del rotor es el uso de 2 juegos de poleas colocados a ambos lados del prototipo y 4 trozos de hilo. Cada juego se compondría básicamente de una polea grande a la que está soldada una polea chica. La polea grande y la chica tienen un mismo eje. En la polea grande va enrollado el hilo que sujeta a la tapita. La polea grande gira al descender la tapita. Al girar la polea chica, el hilo de la polea del rotor se desenrolla girando el rotor y se enrolla en la polea chica.
Para verificar que no se trata solamente de una disminución de potencia con incremento de velocidad por la transformación realizada por los imanes de una parte del par en velocidad, sino que el incremento en la velocidad de giro es producido conjuntamente por el trabajo extra neto de los imanes, vamos a calcular la magnitud del trabajo extra neto con la ayuda del sistema de pesos y poleas.
Procedamos a calcular primero el trabajo de la fuerza magnética por encarrilamiento. Enrollemos al revés los hilos en las poleas del rotor. De este modo la acción de la fuerza magnética por encarrilamiento levantará los pesos. El trabajo realizado al levantar los pesos será el trabajo de la fuerza magnética por encarrilamiento. El valor de los pesos debe ser lógicamente la carga máxima que las 2 fuerzas magnéticas por encarrilamiento pueden levantar. Experimentando encontré que la carga máxima es de 6 monedas por tapita. Las tapitas no se apoyarán en ningún momento en el suelo.
Una vez preparado el sistema de pesos y poleas, desplacemos el rotor hasta que actúe la fuerza magnética por encarrilamiento. Puesto que los 2 imanes pequeños están en fase, lo que experimenta uno lo experimenta el otro al mismo tiempo, por lo tanto, en los cálculos de la altura de elevación nos concentraremos en lo que le ocurra a uno de los imanes pequeños. Marcamos el punto desde el cual comenzó a actuar la fuerza magnética por encarrilamiento y el punto en el cual se detiene el imán pequeño, y medimos con una regla la distancia entre los 2 puntos. Considerando la trayectoria circular que describe el imán pequeño, la distancia medida constituye matemáticamente un secante. A partir de la longitud de la secante cálculamos la longitud del arco descrito por el imán pequeño cuando actúa sobre él la fuerza magnética por encarrilamiento
La = 3,1416 r arcsen (Ls/2r) / 90º
donde,
La = longitud del arco
Ls = longitud de la secante
r = radio de la trayectoria del imán pequeño
La1 = 3,1416 (0,0985 m) arcsen [0,045m/2(0,0985 m)] / 90º
= 3,1416 (0,0985 m) (13,2º) / 90º
= 0,0454 m
Calcularemos el perímetro de la trayectoria del imán pequeño y el perímetro de los canales de la polea el rotor con la fórmula
perímetro = 2 (3,1416) r
donde,
r = radio
perímetro de la trayectoria = 2 (3,1416) (0,0985 m)
= 0,6189 m
perímetro de los canales de la polea = 2 (3,1416) (0,0055 m)
= 0,0346 m
Usando los valores de los perímetros de la trayectoria y de los canales de la polea del rotor en una regla de tres, obtenemos la longitud del arco descrito por cada canal
0,6189 m ---- 0,0454 m
0,0346 m ---- 0,0025 m
En este caso la longitud del arco de cada canal es de 0,0025 m. La longitud del arco de cada canal es igual a la altura h a la que son elevadas las cargas. Con el peso de las cargas y la altura a la que son elevadas, calculamos el trabajo de las 2 fuerzas magnéticas por encarrilamiento
T = W h
donde,
T = trabajo de las 2 fuerzas magnéticas por encarrilamiento
W = peso de las 2 cargas
h = altura de elevación de cada carga
T1 = W h1
= [ (2) (0,0263 N) + (6) (2) (0,0247 N)] (0,0025 m)
= (0,349 N) (0,0025 m)
= 0,00087 J
Ahora calculemos los trabajos de las fuerzas repulsiva y atractiva. Para ello desenrollaremos los hilos de la polea del rotor y los enrollaremos en sentido contrario. Los extremos libres de los hilos los pasamos por los canales alternos de las poleas de los soportes. El peso de las cargas debe mantenerse igual.
Desplazamos el rotor en sentido contrario al anterior hasta que actúe la fuerza magnética de atracción. Marcamos el punto desde el cual comenzó a actuar la fuerza de atracción y el punto en el cual se detiene el imán pequeño. Medimos con la regla la distancia entre aquellos 2 puntos. Repitiendo los pasos anteriores calculamos el trabajo de las 2 fuerzas magnéticas de atracción.
La2 = 3,1416 (0,0985 m) arcsen [o,014 m / 2 (0,0985 m)] / 90°
= 3,1416 (0,0985 m) (4°) / 90°
= 0,0138 m
0,6189 m ---- 0,0138 m
0,0346 m ---- 0,0008 m
T2 = W h2
= (0,349 N) (0,0008 m)
= 0,00028 J
Una vez calculado el trabajo de las fuerzas atractivas proseguiremos con el cálculo del trabajo de las 2 fuerzas magnéticas de repulsión. Desplazamos el brazo en contra de la fuerza magnética por encarrilamiento hasta que actúe la fuerza de repulsión. Marcamos el punto desde el cual comenzó a actuar la fuerza de repulsión y el punto en el cual se detiene el imán pequeño. Medimos con la regla la distancia entre aquelos dos puntos y cálculamos el trabajo de las fuerzas repulsivas.
La3 = 3,1416 (0,0985 m) arcsen [0,02 m/2 (0,0985 m)] / 90°
= 3,1416 (0,0985 m) (5,8°) / 90°
= 0,0199 m
0,6189 m ---- 0,0199 m
0,0346 m ---- 0,0011 m
T3 = W h3
= (0,349 N) (0,0011 m)
= 0,00038 J
En la fig. 28 se aprecia que las posiciones iniciales y finales no coinciden. Los retrasos de las posiciones iniciales y los adelantos de las posiciones finales son una consecuencia del uso de cargas.
Recordemos que la longitud del arco descrito por la polea del rotor fue de 0,0025 m con la fuerza magnética por encarrilamiento, de 0,0008 m con la fuerza de atracción y de 0,0011 m con la fuerza de repulsión. Las pérdidas de energía por fricción están relacionadas con la longitud de estos arcos, puesto que la fricción se produce entre el rotor y el cilindro de madera de balsa sobre el que se apoya. Podemos asumir entonces que la energía perdida cuando actúan las fuerzas magnéticas por encarrilamiento (Pf1) es igual a la suma de las pérdidas con las fuerzas de atracción (Pf2) y de repulsión (Pf3), o sea
Pf1 = Pf2 + Pf3
Pf1- Pf2 - Pf3 = 0
Cómo las pérdidas de energía por fricción se compensan entre ellas mismas, el trabajo extra neto (Tn) producido en cada media vuelta al girar el rotor en el sentido en que actúan las fuerzas magnéticas por encarrilamiento, es simplemente igual al trabajo de las 2 fuerzas magnéticas por encarrilamiento (T1) menos la suma de los trabajos de las 2 fuerzas atractivas (T2) con los trabajos de las 2 fuerzas repulsivas (T3),
Tn = T1 - (T2 + T3)
= T1 - T2 - T3
= 0,00087 J - 0,00028 J - 0,00038 J
= 0,00021 J
Si bien el valor del trabajo extra neto es muy pequeño en relación a lo esperado de un móvil perpetuo (se requieren 2381 vueltas para obtener apenas 1 J), creo que a nadie que haya leído este blog le quepará la menor duda de que la torca de los imanes merece ser estudiada más a fondo.
